Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 최종합격후기
- 자료구조
- 이분탐색
- Algorithm
- 알고리즘
- DivideandConquer
- 프로그래머스
- SAP CERTI
- ABAP NetWeaver 7.50
- programmers
- ABAP CERTIFICATION
- insertion
- codingTest
- 너비우선탐색
- sort
- 정렬
- kakao
- binarysearch
- 백준
- Baekjoon
- datastructure
- DynamicProgramminng
- 동적계획벅
- Altorithm
- kakaoblind
- sap abap
- 분할정복
- LinkdeList
- CJ올리브네트웍스
- SAP CERTIFICATION
Archives
- Today
- Total
서랑의 개발 블로그
[알고리즘] 04. 이분 탐색(Binary Search) 본문
<본 포스팅은 개인 공부 목적으로 작성되었습니다.>
✅ 이분 탐색(Binary Search)
이진 탐색이라고도 불리며 이미 정렬된 데이터에서 특정 값을 찾을 때 절반 씩 나눠가며 찾는 알고리즘이다.
- 분할 정복 알고리즘 (Divide and Conquer)
- Divide(분할) : 문제를 하나 또는 둘 이상으로 나눈다.
- Conquer(정복) : 나눠진 문제가 충분히 작고, 해결이 가능하다면 해결하고 아니면 또 나눈다.
- 이분 탐색(Binary Search)
- Divide(분할) : 정렬된 데이터를 절반으로 나눈다.
- Conquer(정복)
- 검색할 값(Search) > 중간값이면 오른쪽에서 다시 데이터를 찾는다.
- 검색할 값(Search) < 중간값이면 왼쪽에서 다시 데이터를 찾는다.
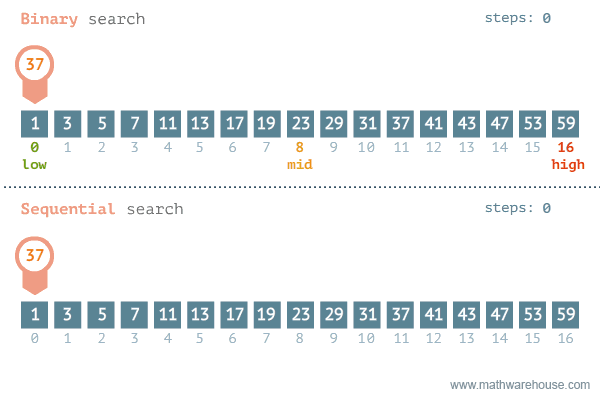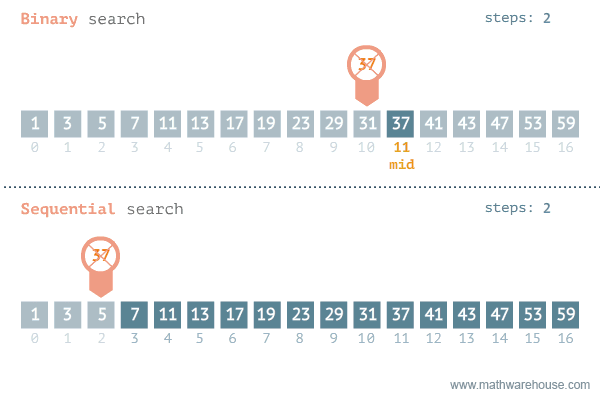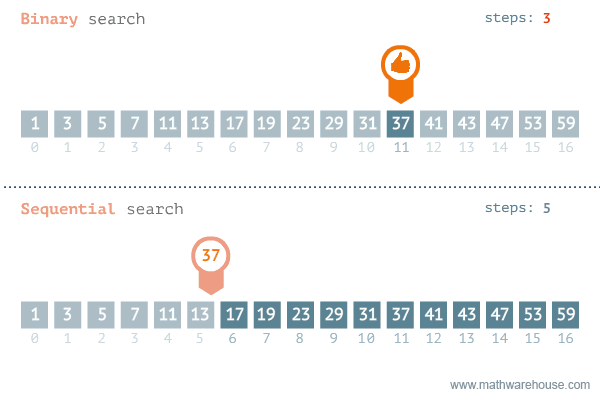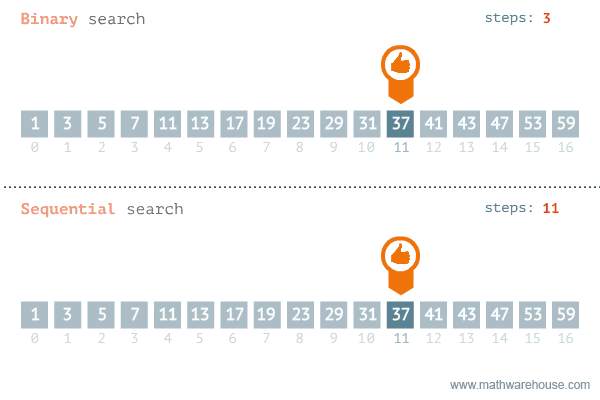
출처 - https://blog.penjee.com/binary-vs-linear-search-animated-gifs/
순차 탐색과 비교를 하면 이분 탐색은 절반씩 나눠가며 탐색을 하기 때문에 순차 탐색보다 훨씬 빠르다는 것을 알 수 있다.
✔ 이분 탐색 구현
- 이분 탐색을 하기 위해서는 일단 정렬된 데이터여야만 한다.
- 정렬된 데이터중 가장 작은 값을 left, 큰 값을 right, middle값을 left와 right의 중간값으로 설정한다.
- 탐색하고자 하는 데이터를 k라 한다면 k와 middle값을 비교한다.
- k > middle일 경우 데이터는 오른쪽에 있다는 뜻이므로 left값을 middle + 1로 바꾼다.
- k < middle일 경우 데이터는 왼쪽에 있다는 뜻이므로 right값을 middle - 1로 바꾼다.
- 새롭게 설정된 left와 right로 middle값도 다시 설정 후 1 - 3을 반복한다.
✔ 코드
#include <iostream>
using namespace std;
int main(void) {
int arr[] = { 1, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59 };
int target = 37;
int left = 0;
int right = 16;
int mid;
bool flag = true;
while (left <= right) {
mid = (left + right) / 2;
if (arr[mid] == target) {
flag = false;
break;
}
else if (arr[mid] > target) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
if (flag) cout << -1;
else cout << mid + 1;
}위에 그림을 코드로 구현해 보았다. target, left, right, mid값을 설정하고 값이 없을 경우를 위해 flag도 선언해 주었다. while문을 돌면서 mid의 값과 target을 비교해 주었고 만약 같다면 flag를 false로 바꾸고 break 해 주었다. 값이 없다면 -1 있다면 mid는 0부터 시작했으므로 mid + 1을 출력해주었다.
✔ 결과
12✔ 시간 복잡도
- O(log N)
참고자료
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 05. 동적계획법(Dynamic Programming) & 분할정복(Divide and Conquer) (0) | 2021.08.19 |
|---|---|
| [알고리즘] 03. BFS&DFS (0) | 2021.08.15 |
| [알고리즘] 02. 정렬(퀵 정렬, 병합정렬) (0) | 2021.08.13 |
| [알고리즘] 01. 정렬(선택 정렬, 버블 정렬, 삽입 정렬) (0) | 2021.08.11 |
Comments
